Na rozdíl od standardní odchylky je druhá odmocnina numerické hodnoty získané při výpočtu rozptylu. Mnoho lidí kontrastuje s těmito dvěma matematickými koncepty. Tento článek se proto pokouší vrhnout světlo na důležitý rozdíl mezi rozptylem a směrodatnou odchylkou.
Srovnávací graf
| Základ pro porovnání | Odchylka | Standardní odchylka |
|---|---|---|
| Význam | Variance je číselná hodnota, která popisuje variabilitu pozorování z jeho aritmetického průměru. | Standardní odchylka je měřítkem rozptylu pozorování v rámci souboru dat. |
| Co je to? | Je to průměr čtvercových odchylek. | Je to střední průměrná odchylka. |
| Označeno jako | Sigma-kvadrát (σ ^ 2) | Sigma (σ) |
| Vyjádřen v | Čtvercové jednotky | Stejné jednotky jako hodnoty v souboru dat. |
| Označuje | Jak daleko jsou jednotlivci ve skupině rozptýleni. | Kolik pozorování souboru dat se liší od jeho průměru. |
Definice odchylky
Ve statistice je rozptyl definován jako míra variability, která reprezentuje, jak daleko jsou členové skupiny rozděleni. Zjistí průměrnou míru, do které se každé pozorování liší od průměru. Když je rozptyl datového souboru malý, ukazuje blízkost datových bodů k průměru, zatímco větší hodnota rozptylu představuje, že pozorování jsou velmi rozptýlená kolem aritmetického průměru a od sebe navzájem.
Nezařazené údaje :
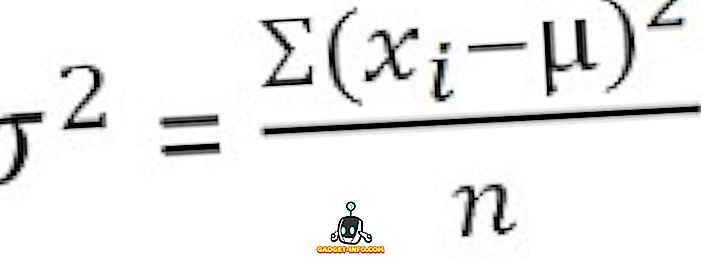
Pro skupinové rozložení frekvence :
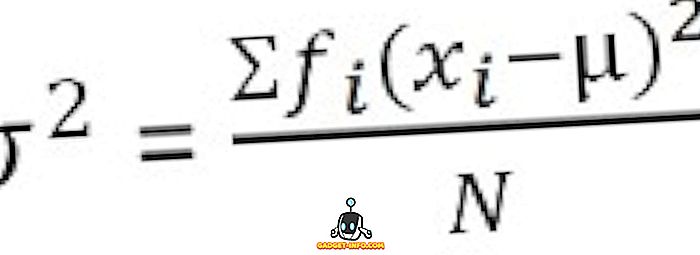
Definice standardní odchylky
Standardní odchylka je míra, která kvantifikuje množství rozptylu pozorování v souboru dat. Nízká směrodatná odchylka je ukazatelem těsnosti skóre k aritmetickému průměru a vysoká směrodatná odchylka představuje; výsledky jsou rozptýleny ve vyšším rozsahu hodnot.
Nezařazené údaje :

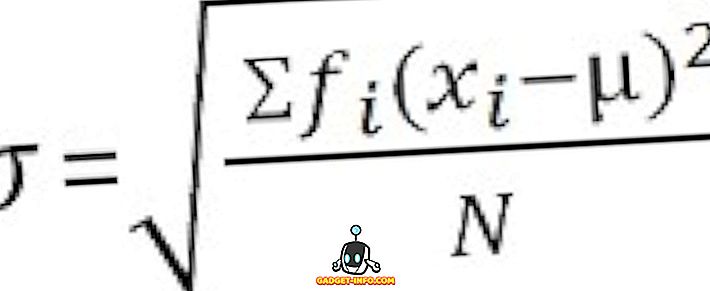
Klíčové rozdíly mezi odchylkou a standardní odchylkou
Rozdíl mezi směrodatnou odchylkou a rozptylem lze jasně stanovit z následujících důvodů: \ t
- Variance je číselná hodnota, která popisuje variabilitu pozorování z jeho aritmetického průměru. Standardní odchylka je měřítkem rozptylu pozorování v rámci souboru dat.
- Odchylka není nic jiného než průměr čtvercových odchylek. Na druhé straně, směrodatná odchylka je průměrná čtvercová odchylka.
- Varianta je označena sigma-kvadrát (σ2), zatímco standardní odchylka je označena jako sigma (σ).
- Odchylka je vyjádřena v čtvercových jednotkách, které jsou obvykle větší než hodnoty v daném souboru dat. Na rozdíl od standardní odchylky, která je vyjádřena ve stejných jednotkách jako hodnoty v souboru dat.
- Variance měří, jak daleko jsou jednotlivci ve skupině rozloženi. Naopak standardní odchylka měří, kolik pozorování sady dat se liší od jejího průměru.
Ilustrace
Známky zaznamenané studentem v pěti předmětech jsou 60, 75, 46, 58 a 80. Musíte zjistit standardní odchylku a rozptyl.
Nejdříve musíte zjistit průměr,

Průměrné průměry jsou tedy 63, 8
Nyní vypočítejte rozptyl
| X | A | (xA) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63, 8 | -3, 8 | 14, 44 |
| 75 | 63, 8 | 11.2 | 125, 44 |
| 46 | 63, 8 | -17, 8 | 316, 84 |
| 58 | 63, 8 | 5.8 | 33, 64 |
| 80 | 63, 8 | 16.2 | 262, 44 |
Kde, X = Pozorování
A = aritmetický průměr
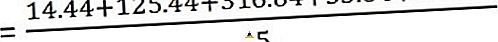
A standardní odchylka je -

Podobnosti
- Variance i směrodatná odchylka jsou vždy pozitivní.
- Pokud jsou všechna pozorování v souboru dat identická, pak směrodatná odchylka a rozptyl budou nulové.
Závěr
Jedná se o základní statistické pojmy, které hrají v různých odvětvích zásadní úlohu. Standardní odchylka je výhodnější než střední hodnota, protože je vyjádřena ve stejných jednotkách jako u měření, zatímco odchylka je vyjádřena v jednotkách větších než daný soubor dat.