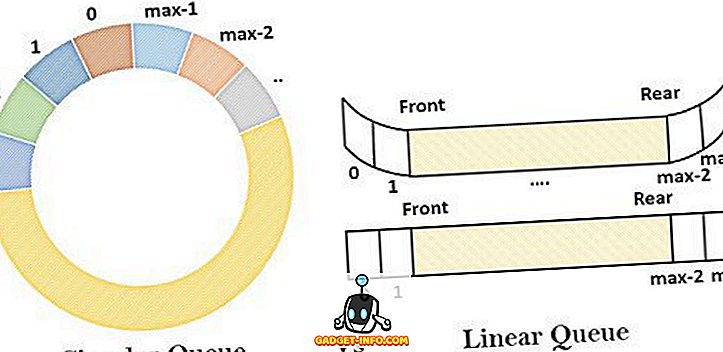
Fronta může být popsána jako primitivní lineární datová struktura podle pořadí FIFO, ve kterém jsou datové prvky vloženy z jednoho konce (zadní konec) a vymazány z druhého konce (přední konec). Dalšími variantami fronty jsou kruhová fronta, dvojnásobně ukončená fronta a prioritní fronta.
Srovnávací graf
| Základ pro srovnání | Lineární fronta | Kruhová fronta |
|---|---|---|
| Základní | Uspořádá datové prvky a instrukce po sobě. | Uspořádá data v kruhovém vzoru, kde je poslední prvek připojen k prvnímu prvku. |
| Pořadí provedení úkolu | Úkoly jsou prováděny tak, aby byly umístěny dříve (FIFO). | Může se změnit pořadí provádění úkolu. |
| Vložení a vymazání | Nový prvek je přidán ze zadní strany a vyjmut z přední strany. | Vložení a odstranění může být provedeno v libovolné poloze. |
| Výkon | Neefektivní | Pracuje lépe než lineární fronta. |
Definice lineární fronty
Lineární fronta je racionálně první v pořadí první . Je tzv. Lineární, protože se podobá přímce, kde jsou prvky umístěny jeden po druhém. Obsahuje homogenní kolekci prvků, do kterých jsou přidány nové prvky na jednom konci a vymazány z jiného konce. Koncept fronty lze chápat na příkladu fronty diváků čekajících mimo pokladní pult pro získání vstupenky do divadla. V této frontě se osoba připojí k zadnímu konci fronty, aby převzala jízdenku a jízdenka je vydána na předním konci fronty.
Ve frontě je několik operací
- Za prvé je fronta inicializována na nulu (tj. Prázdná).
- Určete, zda je fronta prázdná nebo ne.
- Určete, zda je fronta plná nebo ne.
- Vložení nového prvku ze zadní strany (Enqueue).
- Vymazání prvku z přední strany (Dequeue).
Frontu lze implementovat dvěma způsoby
- Staticky (pomocí polí)
- Dynamicky (pomocí ukazatelů)
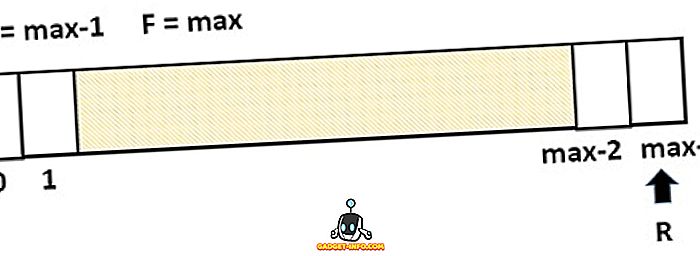
Omezení lineární fronty spočívá v tom, že vytváří scénář, ve kterém nelze do fronty přidávat žádný nový prvek, i když fronta obsahuje prázdná místa. Tato výše uvedená situace je znázorněna na obrázku níže. Zadní strana směřuje k poslednímu indexu, zatímco všechna pole jsou stále prázdná.
Definice kruhového frontu
Kruhová fronta je varianta lineární fronty, která účinně překonává omezení lineární fronty. V kruhové frontě je nový prvek přidán na úplně první pozici fronty, pokud je poslední obsazená a prostor je k dispozici. Pokud jde o lineární frontu, vložení může být provedeno pouze ze zadního konce a vymazání z přední strany. V celé frontě po provedení série po sobě jdoucích vymazání ve frontě vzniká určitá situace, kdy nelze přidat nový prvek, i když je prostor k dispozici, protože podmínka underflow (Rear = max - 1) stále existuje.
Kruhová fronta spojuje dva konce přes ukazatel, kde první prvek přichází za poslední prvek. To také udržuje stopu přední a zadní tím, že implementuje nějakou extra logiku tak že to mohlo stopovat elementy, které mají být vloženy a vymazány. Tímto způsobem kruhová fronta negeneruje podmínku přetečení, dokud není fronta plná.
Některé podmínky následované kruhovou frontou:
- Přední strana musí ukazovat na první prvek.
- Fronta bude prázdná, pokud Front = Rear.
- Při přidání nového prvku se fronta zvýší o hodnotu jedna (Rear = Rear + 1).
- Když je prvek z fronty smazán, přední se zvýší o jednu (Front = Front + 1).
Klíčové rozdíly mezi lineárním a kruhovým fronty
- Lineární fronta je uspořádaný seznam, ve kterém jsou datové prvky organizovány v sekvenčním pořadí. Naproti tomu kruhová fronta ukládá data kruhovým způsobem.
- Lineární fronta následuje příkaz FIFO pro provedení úlohy (prvek přidaný na první pozici bude vymazán v první pozici). Naopak v kruhové frontě se může měnit pořadí operací prováděných na prvku.
- Vkládání a mazání prvků je fixováno v lineární frontě, tj. Přidávání ze zadního konce a mazání z předního konce. Na druhé straně je kruhová fronta schopna vkládat a mazat prvek z libovolného místa, dokud není neobsazena.
- Lineární fronta ztrácí paměťový prostor, zatímco kruhová fronta umožňuje efektivní využití prostoru.
Implementace lineární fronty
Níže uvedený algoritmus ilustruje přidávání prvků do fronty:
Fronta potřebuje tři datové proměnné včetně jednoho pole pro uložení fronty a jiné pro uložení přední a zadní počáteční pozice, která je -1.
insert (položka, fronta, n, zadní) {if (zadní == n) pak vytiskne "přetečení fronty"; jinde {zadní = zadní + 1; fronta [zadní] = položka; }} Níže uvedený algoritmus ilustruje odstranění prvků ve frontě:
delete_circular (položka, fronta, vzadu, vpředu) {if (zadní == front) pak tisknout "underflow fronty"; else {front = front + 1; item = fronta [front]; }} Realizace kruhové fronty
Algoritmus pro interpretaci přidání prvku do kruhové fronty:
insert_circular (položka, fronta, zadní, přední) {zadní = (zadní + 1) mod n; jestliže (přední == zadní) pak tisk “fronta je plná”; else {fronta [zadní] = položka; }} Algoritmus vysvětluje odstranění prvku v kruhové frontě:
delete_circular (položka, fronta, vzadu, vpředu) {if (front == vzadu) pak tisk ("fronta je prázdná"); else {front = front + 1; item = fronta [front]; }} Závěr
Lineární fronta je neúčinná v určitých případech, kdy jsou prvky potřebné k přesunu do volných prostorů za účelem provedení operace vkládání. To je důvod, proč má tendenci plýtvat úložným prostorem, zatímco kruhová fronta vhodně využívá úložný prostor, protože prvky jsou přidávány v libovolné poloze, pokud existuje prázdný prostor.



![Parodie sociálních médií [Video]](https://gadget-info.com/img/best-gallery/213/parody-social-media.jpg)





